MATH225N Week 4: Evaluating Probability With the Binomial Distribution

MATH225N Week 4: Evaluating Probability With the Binomial Distribution

A basketball player has a 0.603 probability of making a free throw. If the player shoots 28 free throws, what is the probability that she makes no more than 20 of them? (Round your answer to 3 decimal places if necessary.)

Ans: 0.921

The probability of winning on an arcade game is 0.673. If you play the arcade game 17 times, what is the probability of winning exactly 8 times? Round your answer to three decimal places.

Ans: P(X=8)=0.044

Give the numerical value of the parameter n in the following binomial distribution scenario.
The probability of buying a movie ticket with a popcorn coupon is 0.597 and without a popcorn coupon is 0.403. If you buy 18 movie tickets, we want to know the probability that no more than 13 of the tickets have popcorn coupons. Consider tickets with popcorn coupons as successes in the binomial distribution. Do not include n= in your answer.

Ans: 18

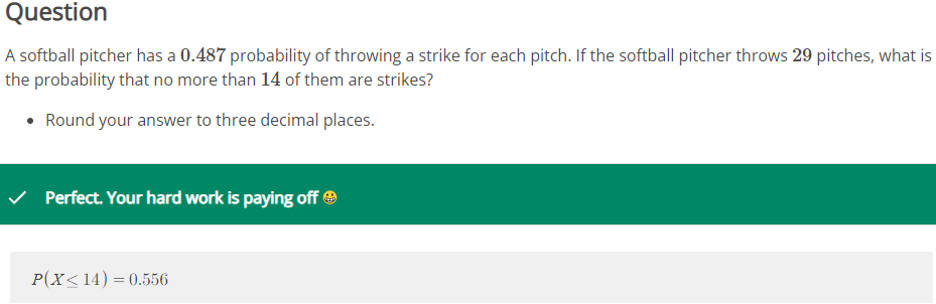
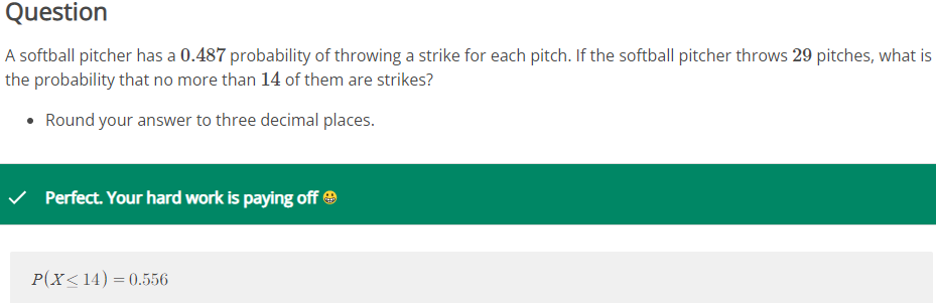
Identify the parameters p and n in the following binomial distribution scenario. A softball pitcher has a 0.579 probability of throwing a strike for each pitch and a 0.421 probability of throwing a ball. If the softball pitcher throws 27 pitches, we want to know the probability that exactly 17 of them are strikes. (Consider strikes as successes in the binomial distribution.)

p=0.421, n=27

p=0.421, n=17

p=0.579, n=17

p=0.579, n=27……………………………purchase entire quiz at $10 only